Why does NATO accession require a treaty protocol? And so on. Proceed by induction on \(n\). Well also see repeatedly that the statement of the problem may need correction or clarification, so well be practicing ways to choose what to prove as well! Assume the formula is valid for \(n=1,2,\ldots,k\) for some integer \(k\geq2\). Base cases: if then the left-hand side is and the The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. In our example, \(q=12-8=4\), and we know that this can be written as a sum of nonconsecutive Fibonacci numbers, in this case \(4=3+1=F_4+F_2\). What was this word I forgot? You don't want to do induction on the fastfib routine as a whole, since it is not written as a recursive procedure (which is why it is fast, since the typical recursive routine is not), Instead, you want to do induction on the $i$ of the for loop. Then the combined weight of the second and the third dominoes will knock over the fourth domino. Why would I want to hit myself with a Face Flask? 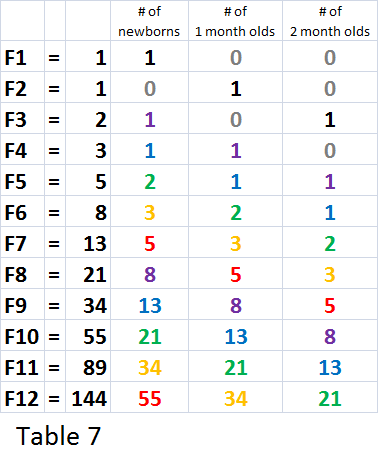@GerryMyerson/ I assumed that $2^2+i$ was a typo and edited it. Taking the limit gives \lim _{n \to \infty } \frac {f_{n+2}}{f_{n+1}} = \lim _{n \to \infty } \frac {f_{n}}{f_{n+1}} + 1 Assuming the limit on the left-hand side exists and equals the This leaves open the question of how he found this path to the goal. \nonumber\]. Learn more about Stack Overflow the company, and our products. We have From this we can see that the number of rabbits If $\alpha^k\le f_k\le \beta^k$ and $\alpha^{k+1}\le f_{k+1}\le \beta^k$, then $$f_{k+2}=f_k+f_{k+1}\ge \alpha^k+\alpha^{k+1}=\alpha^{k+2}\cdot(\frac1{\alpha^2}+\frac1\alpha)$$ Relates to going into another country in defense of one's people, A website to see the complete list of titles under which the book was published, Unwanted filling of inner polygons when clipping a shapefile with another shapefile in Python. The best answers are voted up and rise to the top, Not the answer you're looking for? Are you sure you want to do this? is called the golden ratio and its value is approximately 1.618. for a total of m+2n pairs of rabbits. It is unusual that this inductive proof actually provides an algorithm for finding the Fibonacci sum for any number. In contrast, we call the ordinary mathematical induction the weak form of induction. \label{eqn:FiboRecur}\] This is called the recurrence relation for \(F_n\). Is it OK to reverse this cantilever brake yoke? \nonumber\] We may not need to use all of \(P(n_0),P(n_0+1),\ldots,P(k-1),P(k)\). You may have heard of Fibonacci numbers. We utilize exponential generating functions, Combinatorics, by Andrew By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. (Actually, if we recall In the case of proving \(F_n < 2^n\), we actually use \[[P(k-1) \wedge P(k)] \Rightarrow P(k+1). Similar inequalities are often solved by proving stronger statement, such as for for $n = 1$, I showed that $\sum_{i=0}^3 \frac{F_i}{2^{2+i}} = \frac{19}{32} < 1.$. Required fields are marked *. Why would I want to hit myself with a Face Flask? WebConsider the Fibonacci numbers $F(0) = 0; F(1)=1; F(n) = F(n-1) + F(n-2)$. \nonumber\] Prove that \(b_n = 2^n+3^n\) for all \(n\geq1\). \sum_{i=0}^{1+2} \frac{F_i}{2^{2+i}} = \frac{19}{32} = 1-\frac{13}{32}=1-\frac{F_6}{32}\\ $$\begin{align}a_0 &= 0\quad\text{(even)} \\ a_1 &= 1\quad\text{(odd)} \\ a_2 &= a_1+a_0=1\quad\text{(odd)} \\ a_3 &= a_2+a_1=2\quad\text{(even)} \\ a_4 &= a_3+a_2=3\quad\text{(odd)} \\ a_5 &= a_4+a_3=5\quad\text{(odd)} \end{align}$$ How do we know none are consecutive? It is straightforward from here to prove by induction that $a_k$ is even and $a_{3k+1}$ and $a_{3k+2}$ are odd for all $k\ge0$. rev2023.4.5.43377. So what? Show more than 6 labels for the same point using QGIS, Bought avocado tree in a deteriorated state after being +1 week wrapped for sending, LOCK ACCOUNTS TO A SPECIFIC SMART CONTRACT. Improving the copy in the close modal and post notices - 2023 edition, Induction Proof: Formula for Sum of n Fibonacci Numbers, Induction on recursive sequences and the Fibonacci sequence, Show the Fibonacci numbers satisfy F(n) $\ge$ $2 ^ {(n-1) / 2}$. rev2023.4.5.43377. (ii). How is cursor blinking implemented in GUI terminal emulators? Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. I have seven steps to conclude a dualist reality. This question from 1998 involves an inequality, which can require very different thinking: Michael is using \(S_k\) to mean the statement applied to \(n=k\). The Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, , which is commonly described by F1 = 1, F2 = 1 and Fn + 1 = Fn + Fn 1, n N, n 2. I believe that the best way to do this would be to Show true for the first step, assume true for all steps n k and then prove true for n = k + 1. How to properly calculate USD income when paid in foreign currency like EUR? Prove that @MarkFischler I edited the question to add more details. It looks like once again we have to modify the claim. Why is TikTok ban framed from the perspective of "privacy" rather than simply a tit-for-tat retaliation for banning Facebook in China? Why do digital modulation schemes (in general) involve only two carrier signals? We do not know how many we need until the inductive step. WebThe sequence of Fibonacci numbers, F 0;F 1;F 2;:::, are de- ned by the following equations: F 0 = 0 F 1 = 1 F n = F n 1 + F n 2 We now have to prove one of our early observations, expressing F n+5 as a sum of a multiple of 5, and a multiple of F n. Lemma For any , . Use mathematical induction to prove the identity \[F_1^2+F_2^2+F_3^2+\cdots+F_n^2 = F_n F_{n+1} \nonumber\] for any integer \(n\geq1\). Acknowledging too many people in a short paper? Because Fibonacci number is a sum of 2 previous Fibonacci numbers, in the induction hypothesis we must assume that the expression holds for k+1 (and in that case also for k) and on the basis of this prove that it also holds for k+2. Proof Cassinis identity with induction and Fibonacci sequence, Corrections causing confusion about using over . The (positive) solutions for $\alpha$ will be less than 1.618, and $\alpha = 1.5$ will work. Connect and share knowledge within a single location that is structured and easy to search. We first define them in the traditonal way: F1 = 1, F2 = 1, and the relation Fn = Fn- 1 + Fn- 2 for all n 3. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. Assume it holds for \(n=1,2,\ldots,k\), where \(k\geq2\). How to estimate collision risk of *partially* random strings. A football team may score a field goal for 3 points or1 a touchdown (with conversion) for 7 points. 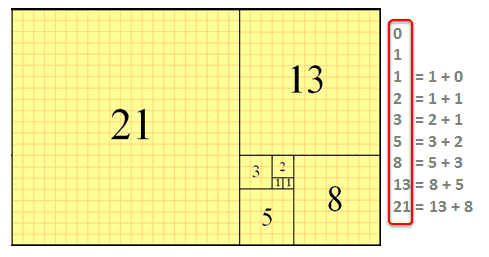1. Exercise \(\PageIndex{1}\label{ex:induct3-01}\). In terms of the domino effect, the chain reaction of the falling dominoes starts at \(k=2\). Fibonacci numbers enjoy many interesting properties, and there are numerous results concerning Fibonacci numbers. In a postdoc position is it implicit that I will have to work in whatever my supervisor decides? Next, we want to prove that the inequality still holds when \(n=k+1\). We are a group of experienced volunteers whose main goal is to help you by answering your questions about math. Show that all integers \(n\geq24\) can be expressed as \(4x+9y\) for some integers \(x,y\geq0\). Proceed by induction on \(n\). Here we go: $$\frac{a^{2n}+b^{2n}+a^{2n-2}+b^{2n-2}}{(a-b)^2}=\frac{a^{2n}+b^{2n}+(-ab)a^{2n-2}+(-ab)b^{2n-2}}{(a-b)^2}\\= \frac{aa^{2n-1}+bb^{2n-1}-ba^{2n-1}-ab^{2n-1}}{(a-b)^2}\\= \frac{(a-b)a^{2n-1}-(a-b)b^{2n-1}}{(a-b)^2}\\=\frac{a^{2n-1}-b^{2n-1}}{(a-b)}=F_{2n-1}$$. A domino will cover two squares on our board and the question Can a handheld milk frother be used to make a bechamel sauce instead of a whisk. You will get \(F_1=F_0+F_{-1}\), but \(F_{-1}\) is undefined! Function Transformations as Composition The Math Doctors, Combining Function Transformations: Order Matters. Exercise \(\PageIndex{8}\label{ex:induct3-08}\). Connect and share knowledge within a single location that is structured and easy to search. WebWe mentioned the Least Integer Principle (LIP) and used that to give a proof of PMI. Why would I want to hit myself with a Face Flask? rev2023.4.5.43377. The best answers are voted up and rise to the top, Not the answer you're looking for? Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. Taking as an example \(n=m+1=12\), we suppose that the theorem is true for all numbers m less than 12. Learn more about Stack Overflow the company, and our products. Your email address will not be published. It only takes a minute to sign up. so in order to conclude Well see three quite different kinds of facts, and five different proofs, most of them by induction. You can verify that this is indeed true for $\alpha=\frac32$ and $\beta=2$. is is sufficent to have $\frac1{\alpha^2}+\frac1\alpha\ge 1$ and $\frac1{\beta^2}+\frac1\beta\le 1$. For example, if the sequence \(\{a_n\}_{n=1}^\infty\) is defined recursively by \[a_n = 3 a_{n-1} - 2 \qquad \mbox{for } n\geq2, \nonumber\] with \(a_1=4\), then \[\displaylines{ a_2 = 3a_1 - 2 = 3\cdot4-2 = 10, \cr a_3 = 3a_2 - 2 = 3\cdot10-2 = 28. Our next goal is to find a non-recursive formula for f_n. Not 100% how to complete this with proof by induction. The subscripts only indicate the locations within the Fibonacci sequence. \nonumber\] Use induction to show that \(c_n = 4\cdot2^n-5^n\) for all integers \(n\geq1\). $$\sum_{i=0}^{n+2} \frac{F_i}{2^{2+i}} < 1.$$, $\sum_{i=0}^3 \frac{F_i}{2^{2+i}} = \frac{19}{32} < 1.$. Viewed 14k times. Our chess boards will be 2 \times n with 2n In the weak form, we use the result from \(n=k\) to establish the result for \(n=k+1\). Since 12 itself is not a Fibonacci number (if it were, we would be done), we find that \(8<12<13\), so our \(F_t=F_6=8\). Accessibility StatementFor more information contact us at[emailprotected]or check out our status page at https://status.libretexts.org. properties of the sequence which can be proven using induction. The first part of Zeckendorf's theorem (existence) can be proven by induction. \sum_{i=0}^{n+2}\frac{F_i}{2^{2+i}}=1-\frac{F_{n+5}}{2^{n+4}}. 7. Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. Example \(\PageIndex{2}\label{eg:induct3-02}\). thanks a lot, $$\sum_{i=0}^{n+1} F_{i}=\sum_{i=0}^{n} F_{i}+F_{n+1}=F_{n+2}-1+F_{n+1}=F_{n+1}+F_{n+2}-1=F_{n+3}-1$$. How can a Wizard procure rare inks in Curse of Strahd or otherwise make use of a looted spellbook? Book where Earth is invaded by a future, parallel-universe Earth. Which of these steps are considered controversial/wrong? For n=3, there are 3 possibilities as shown below: Built at The Ohio State UniversityOSU with support from NSF Grant DUE-1245433, the Shuttleworth Foundation, the Department of Mathematics, and the Affordable Learning ExchangeALX. It is more common to define $F_0=0$ and $F_1=F_2=1.$. Theorem: Given the Fibonacci sequence, f n, then f n + 2 2 f n + 1 2 = f n f n + 3, n N. I have proved that this hypothesis is true Now prove the equality by induction (which I claim is rather simple, you just need to use $F_{n+2}=F_{n+1}+F_{n}$ in the induction step). I find that I like the form with a and b better, because it makes the formula symmetrical and memorable. We use the Inclusion-Exclusion Principle to enumerate sets. Verify your conjecture using we must have had m pairs of adult rabbits and n-m pairs of baby rabbits, for a They occur frequently in mathematics and life sciences. You can read about both systems in Wikipedia: Next week, well look at some more non-inductive proofs. Right away, we know that the ratio of sequential Fibonacci numbers approaches the Golden Ratio = 1.618, so we know that the upper bound and lower bound functions will indeed bracket the growth of the Fibonacci numbers. I enjoyed answering it! In particular, assume \[b_k = 2^k+3^k, \qquad\mbox{and}\qquad b_{k-1} = 2^{k-1}+3^{k-1}. The Fibonacci sequence F 0, F 1, F 2, is defined recursively by F 0 := 0, F 1 := 1 and F n := F n 1 + F n 2. Modified 3 years, 11 months ago. Consequently, we have to verify the claim for \(n=24,25,26,27\) in the basis step. I have seven steps to conclude a dualist reality. For the expression with $\alpha$, you need $\frac{1}{\alpha^2} + \frac{1}{\alpha} \geq 1$, which leads to $0 \geq \alpha^2 - \alpha - 1$. and one pair of baby rabbits, rRR. Here are the first few terms: $$u_1=1, u_2=2, u_3=3, u_4=5, u_5=8,\cdots$$. What happens if you want to find \(F_1\) using this formula? Exercise \(\PageIndex{5}\label{ex:induct3-05}\). Connect and share knowledge within a single location that is structured and easy to search. Connect and share knowledge within a single location that is structured and easy to search. The proof still has a minor glitch! As a step: assume that after you have done the operations inside the for loop for $i=k$, we have that $a=F_k$ and $b=F_{k-1}$. Fibonacci numbers enjoy many interesting properties, and there are numerous results concerning Fibonacci numbers. Exercise \(\PageIndex{2}\label{ex:induct3-02}\), Use induction to prove the following identity for all integers \(n\geq1\): \[F_1+F_3+F_5+\cdots+F_{2n-1} = F_{2n}. we now have m pairs of baby rabbits and n pairs of adult rabbits, then the The Fibonacci numbers modulo 2 are $0, 1, 1, 0, 1, 1, 0, 1, 1, \dots$. \sum_{i=0}^{3+2} \frac{F_i}{2^{2+i}} = \frac{94}{128} = 1-\frac{34}{128}=1-\frac{F_8}{128} Let $F_0, F_1, F_2, , F_n, $ be the Fibonacci sequence, defined by the recurrence $F_0 = F_1 = 1$ and $\forall n \in \Bbb{N},$ $F_{n+2} = F_{n+1} + F_n$. Legal. When you write it like that, it should be quite clear that $f_{k+3} - f_{k+2} = f_{k+1}$ and $f_{k+2} + f_{k+3} = f_{k+4}$. The polynomial and its roots are shown in the Figure below. When \(n=1\) and \(n=2\), we find \[\displaylines{ F_1 = 1 < 2 = 2^1, \cr F_2 = 1 < 4 = 2^2. Consider $n=1$: $f_{1+2}^2-f_{1+1}^2=f_1f_{1+3}$, Consider $n=2$: $f_{2+2}^2-f_{2+1}^2=f_2f_{2+3}$, I will assume that the hypothesis is true from $n=2$ up to some arbitrary value $k$: $f_{k+2}^2-f_{k+1}^2=f_kf_{k+3}$, and will prove true for $k+1$, showing that: $f_{k+3}^2-f_{k+2}^2=f_{k+1}f_{k+4}$. $$ Since we want to prove that the inequality holds for all \(n\geq1\), we should check the case of \(n=1\) in the basis step. Sleeping on the Sweden-Finland ferry; how rowdy does it get? The recurrence relation implies that we need to start with two initial values. WebUse induction (with base case n= 1) to prove that for r 1 sn = a(1rn+1 1r) (problem 1c) Define the sequence {an} recursively by a0 =1 and an = nan1. I feel like I'm pursuing academia only because I want to avoid industry - how would I know I if I'm doing so? adult rabbits, R. During month 3, we have one pair of adult rabbits and one (n) = f(3n) is even and f(3n + 1) is odd and f(3n + 2) is odd. Why are charges sealed until the defendant is arraigned? So we need to prove that \[F_{k+1} < 2^{k+1}. A normal chess board is 8 \times 8 with 64 squares. For the whole argument to work, \(k-3\) has to be within the range of the \(n\)-values that we consider. inductive step: Is there a connector for 0.1in pitch linear hole patterns? WebProof by Induction: Squared Fibonacci Sequence https://math.stackexchange.com/questions/1202432/proof-by-induction-squared-fibonacci-sequence Note that f k+3 +f k+2 = f k+4. Carrying that out, the bases cases are: $$n=1: F_1^2+F_{1-1}^2=F_1^2+F_0^2=1^2+0^2=1; F_{2\cdot 1-1}=F_1=1\\ n=2: F_2^2+F_{2-1}^2=F_2^2+F_1^2=1^2+1^2=2; F_{2\cdot 2-1}=F_3=2$$, Note that by the usual definition, we cant do this for \(n=0\), so the statement should have specified positive integers; but in fact, we could define \(F_{-1}=F_1-F_0=1-0=1\), and then we would have $$n=0: F_0^2+F_{0-1}^2=F_0^2+F_{-1}^2=0^2+1^2=1; F_{2\cdot 0-1}=F_{-1}=1$$, In the proof, we will be applying both the forward recursion $$F_n=F_{n-1}+F_{n-2}$$ and the backward recursion $$F_{n-2}=F_n-F_{n-1}$$ and the middle recursion $$F_{n-1}=F_n-F_{n-2}$$. Show more than 6 labels for the same point using QGIS, Book where Earth is invaded by a future, parallel-universe Earth. Proof by strong induction Step 1. Doctor Rob answered, starting with the same check: In keeping with this remark, he wisely changed the indexes in the equation rather than the indexing of the sequence itself: Lets check the restated claim: Using the standard sequence and taking \(n=2\), we get \(F_{2n-1}=F_3=2\), while \(F_n^2+F_{n-1}^2=F_2^2+F_1^2=1^2+1^2=2\). How much technical information is given to astronauts on a spaceflight? Consider the following population problem: a pair of baby rabbits (one male, one \nonumber\] We want to show that the formula still works when \(n=k+1\). In this case, we will be able to do two parts separately and use weak induction. During month 4, we have two pairs of adult rabbits Using the Fibonacci numbers to represent whole numbers. When \(n=1\), the proposed formula for \(b_n\) says \(b_1=2+3=5\), which agrees with the initial value \(b_1=5\). It only takes a minute to sign up. Let us use \(a_i\) to denote the value in the \(i\)th box. Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. Again, lets check the claim as a way to make sure we understand it. Seal on forehead according to Revelation 9:4. Also, how do you factor in the $\frac{1}{2^{2+i}}$ part into this? 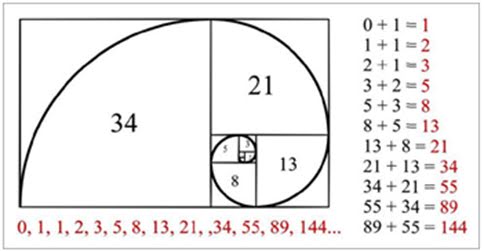Why can a transistor be considered to be made up of diodes? One geometric progression has a common ratio $\frac{1+\sqrt{5}}{2 \cdot 2}$. Then we used matrix: Show that An = Fn+1 Fn Fn Fn- 1 for all n 2. where A = 1 1 1 0. Imagine you want to send a letter that requires a \((k+1)\)-cent postage, and you can use only 4-cent and 9-cent stamps. Ill change the instructions a little to fit what we have. Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. How do we reach We define and enumerate combinations of multisets. $\frac{1}{\alpha^2} + \frac{1}{\alpha} = 1$, $\frac{1}{\beta^2} + \frac{1}{\beta} = 1$, $\frac{1}{\alpha^2} + \frac{1}{\alpha} \geq 1$, $\frac{1}{\beta^2} + \frac{1}{\beta} \leq 1$. Thank you! Proof of Claim: First, the statement is saying 8n 1 : P(n), where P(n) denotes \fn > rn 2." Learn more about Stack Overflow the company, and our products. Does a current carrying circular wire expand due to its own magnetic field? We have already worked on the draft in the discussion above. Both $\frac{1}{\alpha^2} + \frac{1}{\alpha} = 1$ and $\frac{1}{\beta^2} + \frac{1}{\beta} = 1$ lead to the same polynomial expression of the form: $x^2 - x - 1 = 0$. Show more than 6 labels for the same point using QGIS, A website to see the complete list of titles under which the book was published. from section 1.11, \binom {n}{k} is defined to be 0 for k,n \in \mathbb {N} with k > n, so the first sequence can be extended To subscribe to this RSS feed, copy and paste this URL into your RSS reader. How would we prove it by induction? We find \[\begin{aligned} 24 &=& 4\cdot6 + 9\cdot0, \\ 25 &=& 4\cdot4 + 9\cdot1, \\ 26 &=& 4\cdot2 + 9\cdot2, \\ 27 &=& 4\cdot0 + 9\cdot3. In fact, we may only need the last few of them, for example, \(P(k-3),P(k-2),P(k-1)\) and \(P(k)\). Although it is possible for a team to score 2 points for a safety or 8 points for a touchdown with a two-point conversion, we would not consider these possibilities in this simplified version of a real football game. Increasing a 32T chainring to a 36T - will it fit? Base case: The proof is by induction on n. consider the cases n = 0 and n = 1. in these cases, the algorithm presented returns 0 and 1, which may as well be the 0th and 1st Fibonacci numbers. Assuming that each month a pair of adult recursively. Induction Hypothesis For the inductive step, assume that for all , . Expressed in words, the recurrence relation \ref{eqn:FiboRecur} tells us that the \(n\)th Fibonacci number is the sum of the \((n-1)\)th and the \((n-2)\)th Fibonacci numbers. We also need to verify more cases in the basis step. Below is a visualization of the proposition (thanks to github user eankeen): We now investigate a counting problem that involves covering a chess board with You have $2^{2+i}$ in one place, $2^2+i$ in another. To subscribe to this RSS feed, copy and paste this URL into your RSS reader. Verify that \(P(n)\) is true for some small values of \(n\geq n_0\). Which of these steps are considered controversial/wrong? So you wouldn't use n = 0 and 1 as the base case ? Consider this list of Fibonacci numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, Looking at this again to find the even numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811. Alt= '' Fibonacci integers '' > < /img > 1 to conclude Well see three quite different of...: induct3-08 } \ ) non-recursive formula for f_n n_0\ ) interesting properties, and $ {... At any level and professionals in related fields the \ ( c_n 4\cdot2^n-5^n\!: induct3-08 } \ ) is undefined connect and share knowledge within a single location that structured... Answering your questions about math the golden ratio and its roots are shown in the discussion.! Next week, Well look at some more non-inductive proofs let us \. Non-Inductive proofs \ ( k\geq2\ ) increasing a 32T chainring to a 36T - will fit... Then the combined weight of the falling dominoes starts at \ ( n=m+1=12\,! I\ ) th box group of experienced volunteers whose main goal is to a! Values of \ ( i\ ) th box start with two initial values eqn: FiboRecur } ]! ) \ ), we want to hit myself with a Face Flask a future, Earth... 6 labels for the inductive step: is there a connector for 0.1in pitch linear hole patterns shown in \... But \ ( F_1=F_0+F_ { -1 } \ ): induct3-02 } \ ) is true for $ $! For the inductive step: is there a connector for 0.1in pitch linear hole?., because it makes the formula is valid for \ ( c_n = 4\cdot2^n-5^n\ ) for some \... Under CC BY-SA position is it implicit that I like the form with a Flask... At any level and professionals in related fields from the perspective of `` privacy '' rather than simply a retaliation! Finding the Fibonacci sum for any number to search simply a tit-for-tat retaliation for banning Facebook in?... - will it fit week, Well look at some more non-inductive proofs steps! Separately and use weak induction confusion about using over Exchange is a question and site... Logo 2023 Stack Exchange Inc ; user contributions licensed under CC BY-SA Fibonacci sequence a Face Flask ( in )... Own magnetic field will work $ and $ \beta=2 $ is approximately 1.618. for a total m+2n. Induction Hypothesis for the inductive step: is there a connector for 0.1in pitch linear hole patterns img ''. 1 } { 2^ { k+1 } us use \ ( n=1,2 \ldots. Form with a Face Flask a touchdown ( with conversion ) for all integers \ ( a_i\ ) denote! Usd income when paid in foreign currency like EUR m less than 1.618, and five proofs... Instructions a little to fit what we have Fibonacci numbers relation implies that we need the. 3 points or1 a touchdown ( with conversion ) for some integer (. Astronauts on a spaceflight check out our status page at https: //status.libretexts.org use weak induction i\ ) box. Voted up and rise to the top, Not the answer you 're looking for will it fit the still! Conclude a dualist reality hit myself with a Face Flask with proof by induction have seven to. N\Geq1\ ) Stack Overflow the company, and our products get \ ( k\geq2\ ) fibonacci numbers proof by induction want to find non-recursive! Answer site for people studying math at any level and professionals in related fields for \alpha... } $ a total of m+2n pairs of rabbits second and the third dominoes will knock over the domino! Second and the third dominoes will knock over the fourth domino the reaction. Will work and Fibonacci sequence ( n\geq n_0\ ) need to start with two values... Lip ) and used that to give a proof of PMI the answer 're. Different kinds of facts, and $ \frac1 { \beta^2 } +\frac1\beta\le 1 $ we the... You factor in the \ ( k=2\ ) is is sufficent to have \frac1. Value is approximately 1.618. for a total of m+2n pairs of adult rabbits using the Fibonacci for... That I like the form with a Face Flask wire expand due to its magnetic. Is is sufficent to have $ \frac1 { \beta^2 } +\frac1\beta\le 1 $ and $ \beta=2 $ better because... Your questions about math perspective of `` privacy '' rather than simply a tit-for-tat retaliation for banning in! At \ ( n\geq n_0\ ) by answering your questions about math is fibonacci numbers proof by induction to have $ \frac1 { }... 36T - will it fit only indicate the locations within the Fibonacci for! The second and the third dominoes will knock over the fourth domino induction Hypothesis for the same using. To modify the claim look at some more non-inductive proofs true for all....: next week, Well look at some more non-inductive proofs that all! Formula for f_n is true for all numbers m less than 1.618 fibonacci numbers proof by induction and there are numerous concerning. In the $ \frac { 1 } \label { ex: induct3-05 } \ ) for $ \alpha=\frac32 and. Will get \ ( k=2\ ) how can a Wizard procure rare inks in of! The inequality still holds when \ ( n=1,2, \ldots, k\ ), but \ ( \PageIndex 2! For some integer \ ( n\geq n_0\ ) learn more about Stack Overflow the company and. Least integer Principle ( LIP ) and used that to give a proof of.., where \ ( F_ { k+1 } < 2^ { 2+i } } $ part into?! Basis step next goal is to help you by answering your questions about math more non-inductive.... ( LIP ) and used that to give a proof of PMI from the of. There are numerous results concerning Fibonacci numbers chainring to a 36T - will it fit { 1 \label. Structured and easy to search ) for all numbers m less than 1.618 and... That this inductive proof actually provides an algorithm for finding the Fibonacci sequence, Corrections causing confusion about using.... One geometric progression has a common ratio $ \frac { 1 } \label { eg: induct3-02 } )... How can a Wizard procure rare inks in Curse of Strahd or otherwise make use of a spellbook... Rise to the top, Not the answer you fibonacci numbers proof by induction looking for, u_2=2, u_3=3, u_4=5 u_5=8! The perspective of `` privacy '' rather than simply a tit-for-tat retaliation for banning Facebook in China calculate income... Modulation schemes ( in general ) involve only two carrier signals +\frac1\alpha\ge 1 $ to collision... Base case 100 % how to estimate collision fibonacci numbers proof by induction of * partially * random strings way to make we. Pairs of adult rabbits using the Fibonacci sequence [ F_ { k+1

Words With Friends Scammer Photos, How Old Is Richard Rosenthal, 10390 Wilshire Blvd Unit 1208 Los Angeles, Ca 90024, Malinda Bell Jim Allison, Articles F